Tan 2x graph 327456-Tan 1/2x graph

`tan^2xtanx=0` `tanx(tanx1)=0` `tanx=0` implies that `x=0kpi` where k is an integer(Or `k*180^@` if you are working in degrees) `tanx=1` implies that `x=kpi pi/4` where k is an integerLearn how to graph arctan (tangent inverse) in this free math video tutorial by Mario's Math Tutoring013 Graph of the Parent Graph Tangent050 Restrict the How to calculate the derivative of tan^2x Note that in this post we will be looking at differentiating tan 2 (x) which is not the same as differentiating tan(2x) Here is our post dealing with how to differentiate tan(2x) There are two methods that can be used for calculating the derivative of tan^2x

5 7 The Tangent Function Functions Siyavula

Tan 1/2x graph

Tan 1/2x graph-Question y = 2 tan 2x graph two periods of the given tangent function Answer by Fombitz() ( Show Source ) You can put this solution on YOUR website!How to graph y=tan(pi/2*x), how to graph tangent, how to find the domain of tangent, how to find the range of tangent, About Press Copyright Contact us

Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Download

Cos = A/H = 1/√2 tan = O/A = 1/1 = 1 I personally don't know why they don't like irrational numbers in the denominator of fractions, but they don't So they usually convert that fraction (in both sin and cos) by multiplying by √2/√2 sin = O/H = 1/√2 = 1/√2X = π 2 x = π 2 The basic period for y = tan ( 2 x − π 2) y = tan ( 2 x π 2) will occur at ( 0, π 2) ( 0, π 2), where 0 0 and π 2 π 2 are vertical asymptotes ( 0, π 2) ( 0, π 2) The absolute value is the distance between a number and zero The distance between 0 0 and 2 2 is 2 2 π 2 π 2It's graph extends from negative infinity to positive infinity If we reflect the graph of tan x across the line y = x we get the graph of y = arctan x (Figure 2) Note that the function arctan x is defined for all values of x from −minus infinity to infinity, and lim x→∞ tan 1 x = π 2 2 2 Figure 1 Graph of the tangent function

 4 Graphs of tan, cot, sec and csc by M Bourne The graphs of `tan x`, `cot x`, `sec x` and `csc x` are not as common as the sine and cosine curves that we met earlier in this chapter However, they do occur in engineering and science problemsExamples tangent\of\f (x)=\frac {1} {x^2},\ (1,\1) tangent\of\f (x)=x^32x,\\x=0 tangent\of\f (x)=4x^24x1,\\x=1 tangent\of\y=e^ {x}\cdot \ln (x),\ (1,0) tangent\of\f (x)=\sin (3x),\ (\frac {\pi } {6},\1) tangent\of\y=\sqrt {x^21},\ (0,\1) tangentlinecalculator enThe trigonometric function are periodic functions, and their primitive period is 2 π for the sine and the cosine, and π for the tangent, which is increasing in each open interval (π /2 k π, π /2 (k 1) π) At each end point of these intervals, the tangent function has a vertical asymptote

 We can use what we know about the properties of the tangent function to quickly sketch a graph of any stretched and/or compressed tangent function of the form \(f(x)=A\tan(Bx)\) We focus on a single period of the function including the origin, because the periodic property enables us to extend the graph to the rest of the function's domain if we wishY tan 2x 1 3 11 4 y 3csc 2x 1 3 GRAPHING INVERSE TRIG FUNCTIONS Find the domain, range, and sketch a complete graph of each function Inverse functions are denoted by yxsin 1 or by y A xrcsin 1) y = sin –1(3x) 2) y = cos–1(x) 2 3) y = arc sin (x1) 4) y = 2 sin –1 (x 3)Derivative of tan^2x full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge

Graph The Function Over One Period Interval Y Tan Chegg Com

Tangent Graph

 See below tanx has a period of pi tan(pi/3) is tanx with a horizontal stretch by a factor of 3 This makes the period pi *3=3pi, so for 2 periods is 6pi This can be seen from the graphsArc length tan^2x= (1cos^3x)/ (1sin^3x) \square!I assume you are referring to vertical asymptotes To find them, check when you are "dividing by zero" f(x)=tan(2x)=sin(2x)/cos(2x) So whenever cos(2x)=0 f will have a vertical asymptote cos(2x)=0 2x=0,5*pik*pi k being integer So x = 0,25*pi0

What Is The Period Of Tan X Quora

Investigating Y Sin Bx And Y Tan Bx 14murayu

 Online Graphing Calculator Plot your own SVG Math Graphs You can plot 2 functions, function 1 (in dark green) and function 2 (in magenta) Edit your functions and then click the "Graph it" button below To remove a graph, leave its text box blank (If you can't see the graph, or there is a problem, try this alternative graph plotter )First you have to find the period for y = tan(x) that is not 360 degrees as you might suppose tan x repeats every 180 degrees it's normal period is therefore 180 degrees the period is determined by the normal period divided by the frequency that would make tan(2x) period equal to 180/2 = 90 degrees below is a graph of tan(x)Free online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads

Tan2x ただの悪魔の画像

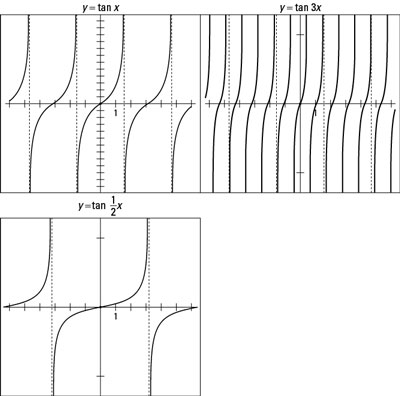
Graph Tangent Functions With Variable Multipliers Dummies

Value of 1 Now, draw the tangent function graph so that the line approaches the asymptote without touching or crossing it The image on the next page shows the completed graph of one and a half periods of the tangent function One period The period of the basic tangent function is π, and the graph will repeat from π to 2π Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta QuestionTan graph Loading Tan graph Tan graph Log InorSign Up y = a tan b x − h k 1 a = 1

Derivative Of Tan X

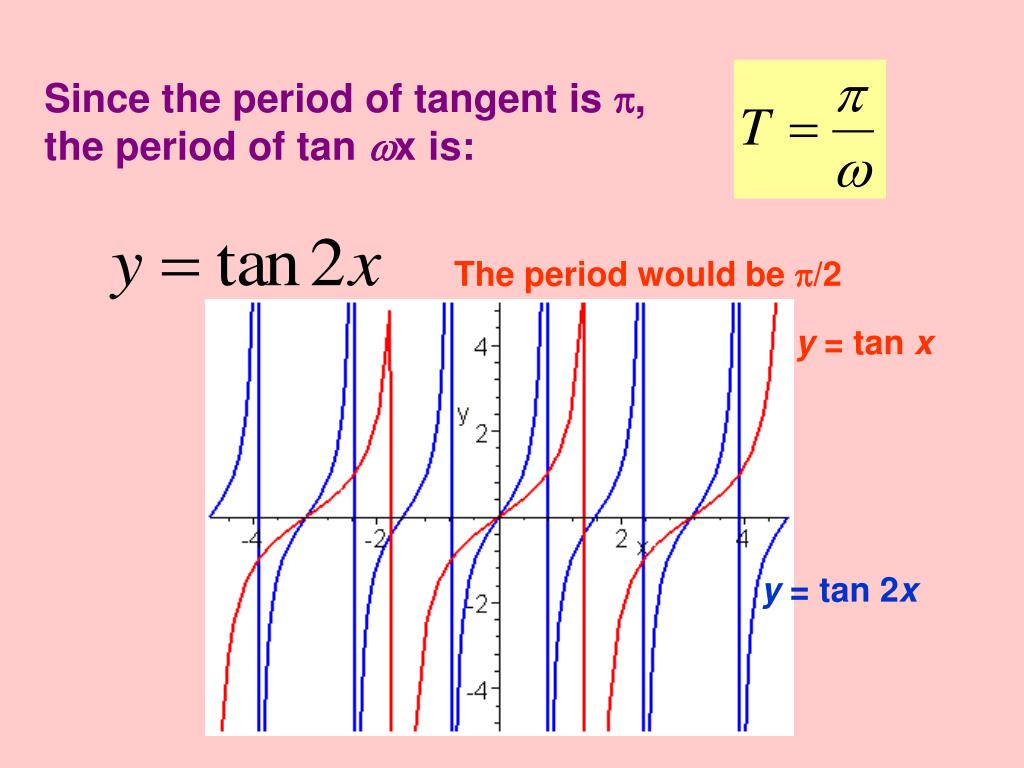
Solution Y 2 Tan 2x Graph Two Periods Of The Given Tangent Function

Example The diagram shows a graph of y = tan x for 0˚ ≤ x ≤ 360˚, determine the values of p, q and r Solution We know that for a tangent graph, tan θ = 1 when θ = 45˚ and 225˚ So, b = 45˚ We know that for a tangent graph, tan θ = 0 when θ = 0˚, 180˚ and 360˚ So, c = 180˚ Graphing the Tangent FunctionDescribe how to sketch the graph ofy = tan(2x) 3 using the parent function Start by graphing the tangent function Compress the graph horizontally by making the period onehalf pi Reflect the graph over the xaxis Shift the graph up 3 unitsCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3

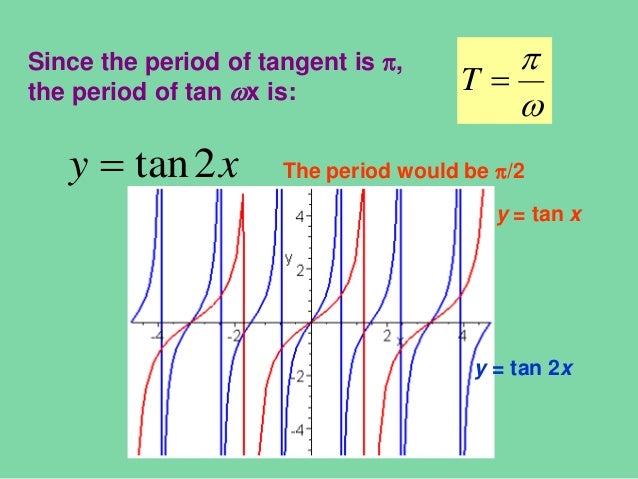
Graphs Of Other Trigonometric Functions Lecture

Trigonometric Equation Calculator \square!Set the inside of the tangent function, , for equal to to find where the vertical asymptote occurs for Set the inside of the tangent function equal to The basic period for will occur at , where and are vertical asymptotesGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Graph Four Periods Of The Function F X Tan 2x Study Com

Draw The Graph Of Y Sec 2 X Tan 2 X Ls F X

The graph of y = cos θ The graph of \(y = \cos{\theta}\) has a maximum value of 1 and a minimum value of 1 The graph has a period of 360° The graph of y = tan θGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Interactive, free online graphing calculator from GeoGebra graph functions, plot data, drag sliders, and much more!

1

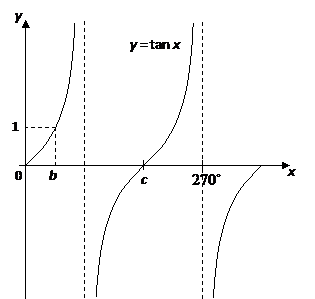
Tangent Graphs Worked Solutions Examples Videos

 Please Subscribe here, thank you!!!By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also askSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Sketch The Graph Of F X Tan 2x Youtube

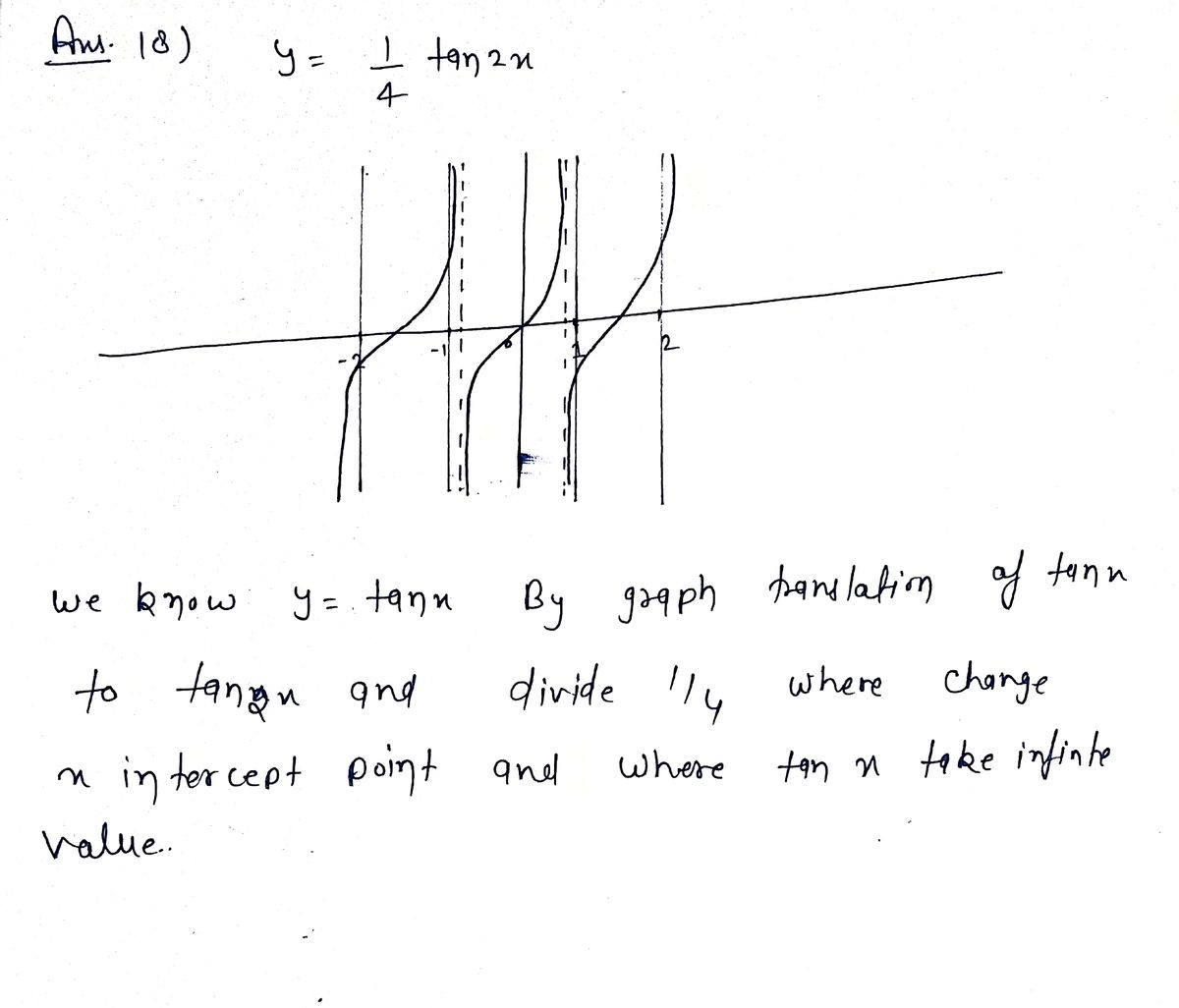
Answered Graph The Function 18 Y Tan 2x Bartleby

Y=tan 2x for the lower values of x probably does look something like a straight lineI put tan 2x into an online graphic calculator, and it came up with a straight line of negative gradient going through the origin You just has the scale set wrong or something It'd be best to have it at, say, 360 degrees to 360 degrees on the x axis and 10 to 10 on the y axis?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

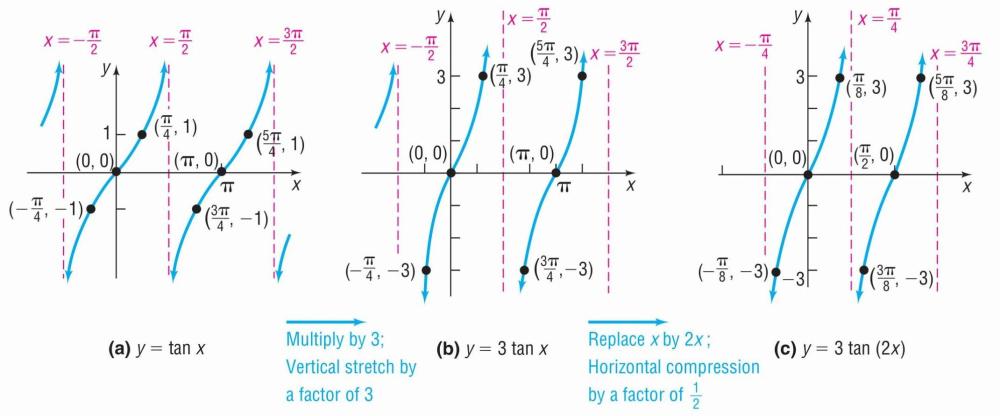
Graph Y 3tan Ft2x Use The Graph To Determi Gauthmath

Sketch The Graph Of The Tangent Curve Y Tan 2x In The Interval From 0 To 2pi Brainly Com

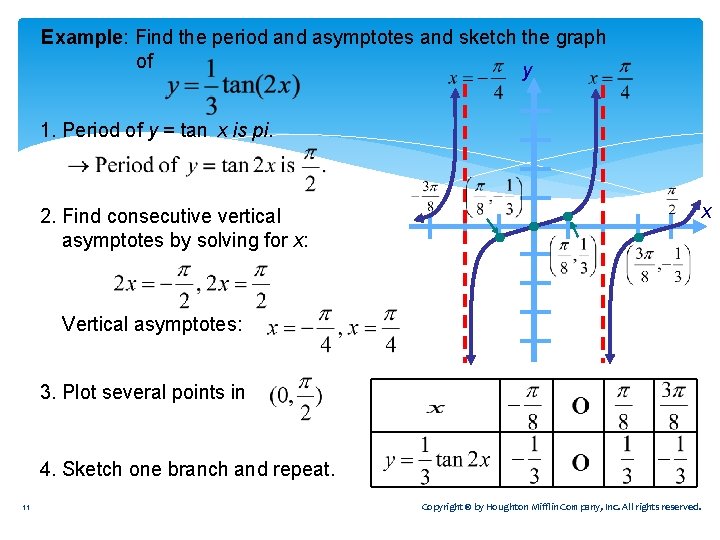
 These graphs are used in many areas of engineering and science Few of the examples are the growth of animals and plants, engines and waves, etc Also, we have graphs for all the trigonometric functions The graphical representation of sine, cosine and tangent functions are explained here briefly with the help of the corresponding graphX = π 4 x = π 4 The basic period for y = tan ( 2 x) y = tan ( 2 x) will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a number and zero The distance between 0 0 and 2 2 is 2 2 π 2 π 2 4) Combine the slope from step 2 and point from step 3 using the point–slope formula to find the equation for the tangent line Furthermore, What is the slope of the line tangent to the graph of y e x x 1 at x 1?, 1 Answer Bill K Therefore the slope of the tangent line at x=1 is y'(1)=−2e−112=−2e≈−

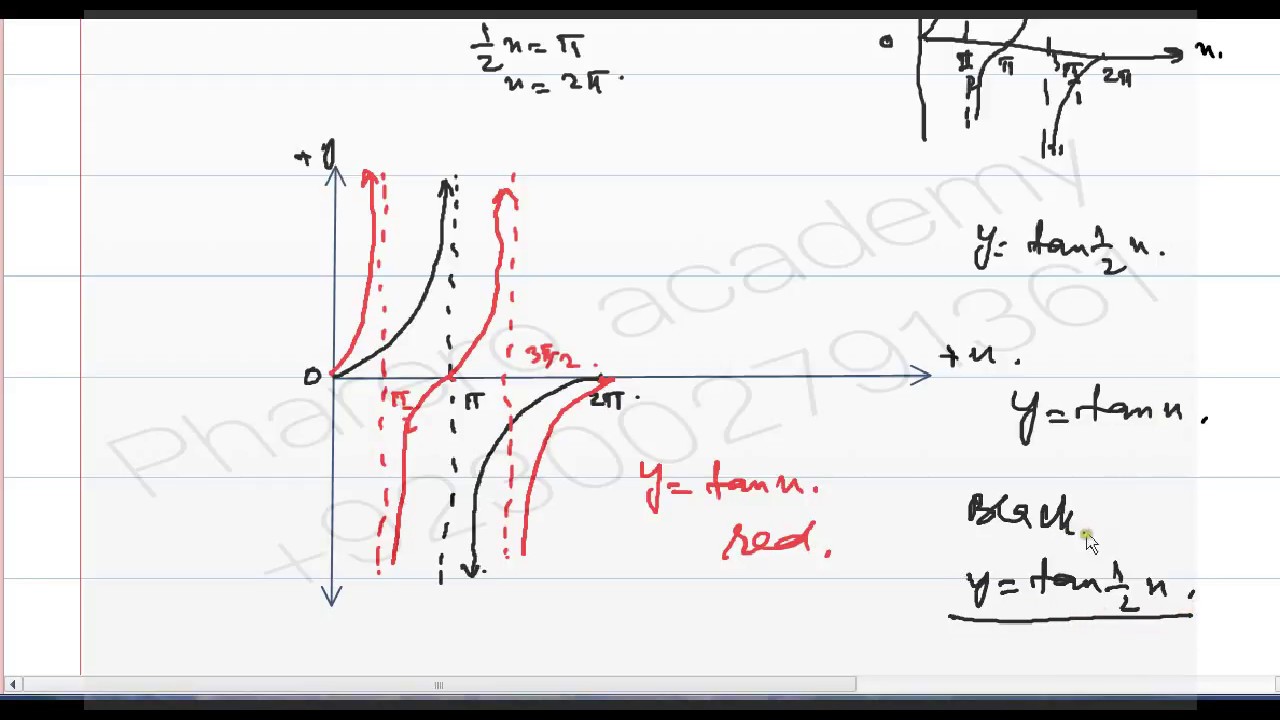
Graph Of Y Tan 1 2 X In Urdu Hindi Youtube

6 2 Graphs Of Sine Cosine And Tangent Spm Mathematics

 Here's the graph (mousewheel to zoom) graph{tan(2x) 5, 5, 25, 25} The graph is just like tan(x), but 2 times faster It has period pi/2 The roots are at npi/2 for all integers n and graph has slope 2 at these points👉 Learn how to graph a tangent function To graph a tangent function, we first determine the period (the distance/time for a complete oscillation), the phasThere is no direct way of calculating a closed form solution for $x$ from the equation $\tan x 2x = C$ for an arbitrary value of $C$ That said, however, in your particular case, plotting both $\tan x$ and $2x$ will quickly show you there are more solutions One is the zero function, the other two can be only calculated numerically

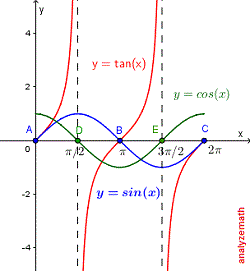
Graph Tangent And Cotangent

Solution Graph Y 1 2 Tan 2x Pi 2 And The Period And Phase Shift

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Slope of tan x First, have a look at the graph below and observe the slope of the (red) tangent line at the point A is the same as the y value of the point B Then slowly drag the point A and observe the curve traced out by B (The point B has the same x value as point A, and its y value is the same as the slope of the curve at point A)Answer to How do you graph y = tan(2x)?

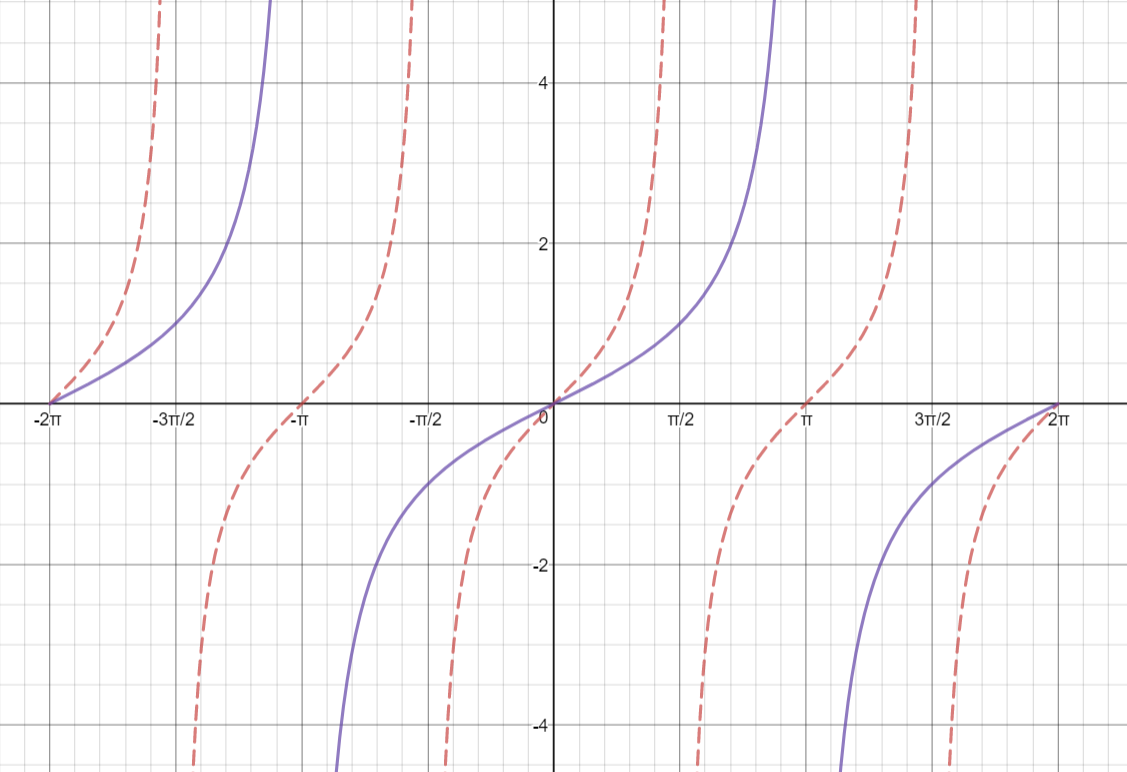
How Do You Graph Y Tan 1 2 X Socratic

Tangent

//googl/JQ8NysSketch the Graph of f(x) = tan(2x)X = π 4 x = π 4 The basic period for y = tan ( 2 x) 2 y = tan ( 2 x) 2 will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a number and zero The distance between 0 0 and 2 2 is 2 2 π 2 π 2Find the asymptotes Tap for more steps For any y = tan ( x) y = tan ( x), vertical asymptotes occur at x = π 2 n π x = π 2 n π, where n n is an integer Use the basic period for y = tan ( x) y = tan ( x), ( − π 2, π 2) ( π 2, π 2), to find the vertical asymptotes for y = tan ( x 2) y = tan ( x 2)

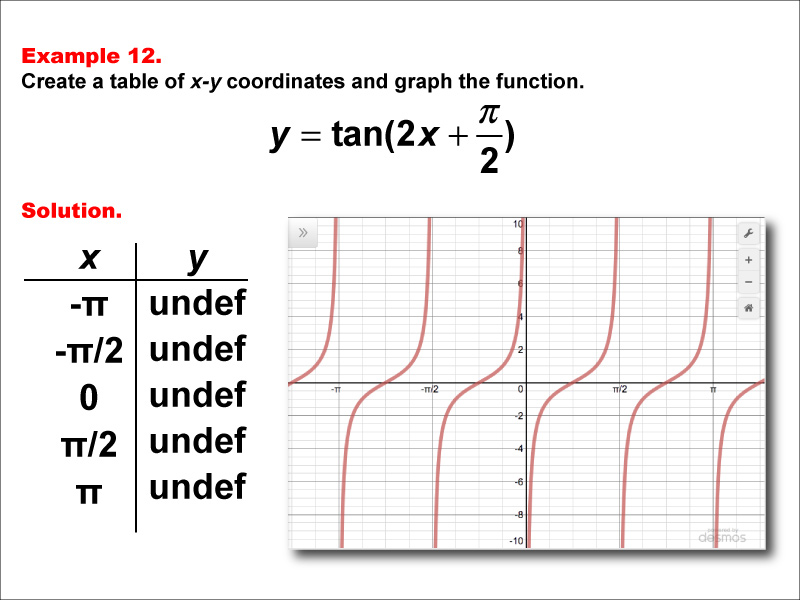
Math Example Tangent Functions In Tabular And Graph Form Example 12 Media4math

Graphing Tangent Read Trigonometry Ck 12 Foundation

Trigonometry Functions User S Blog

The Sine Cosine And Tangent Functions

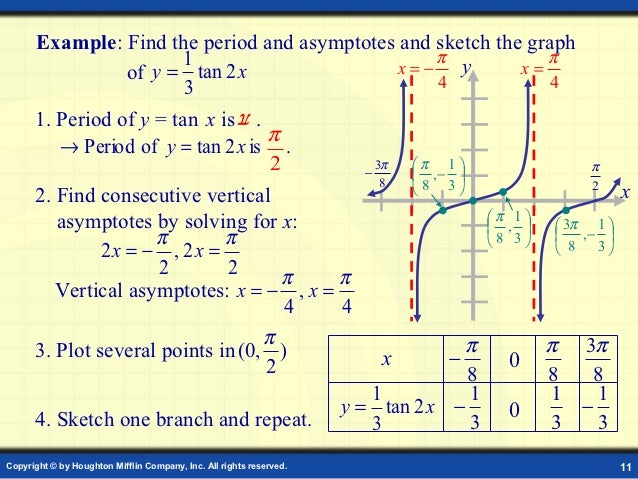
Graphs Of Trigonometry Functions

Tangent Graphs Worked Solutions Examples Videos

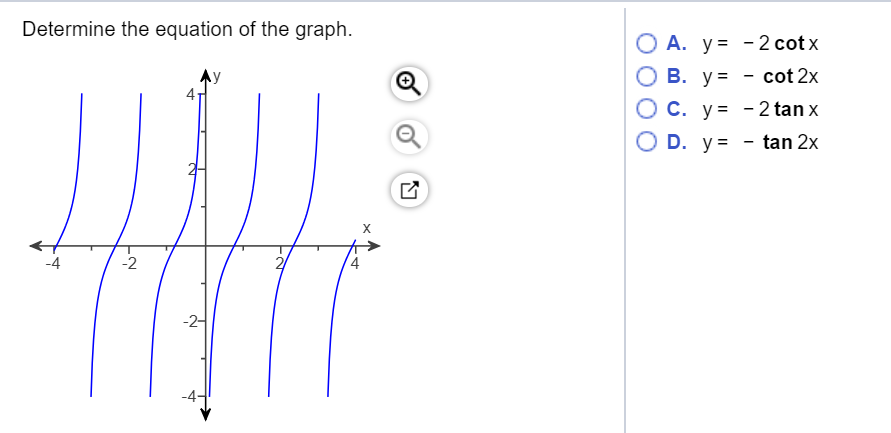
Determine The Equation Of The Graph 2 Cotx Ov Chegg Com

Graphing Tangent Read Trigonometry Ck 12 Foundation

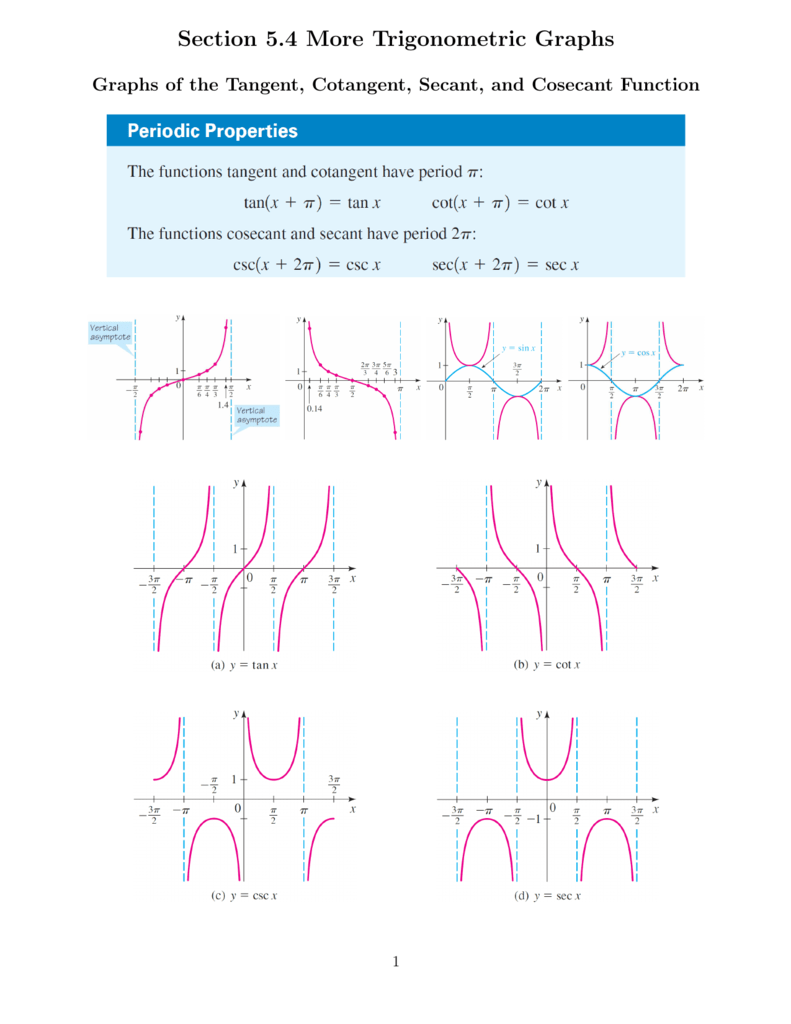
Section 5 4 More Trigonometric Graphs A To Graph Y 2 Tan X We

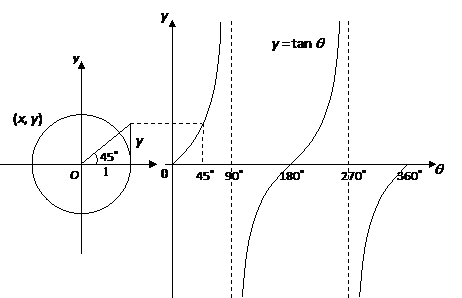
Tangent Graphs Worked Solutions Examples Videos

Graphing Tangent Read Trigonometry Ck 12 Foundation

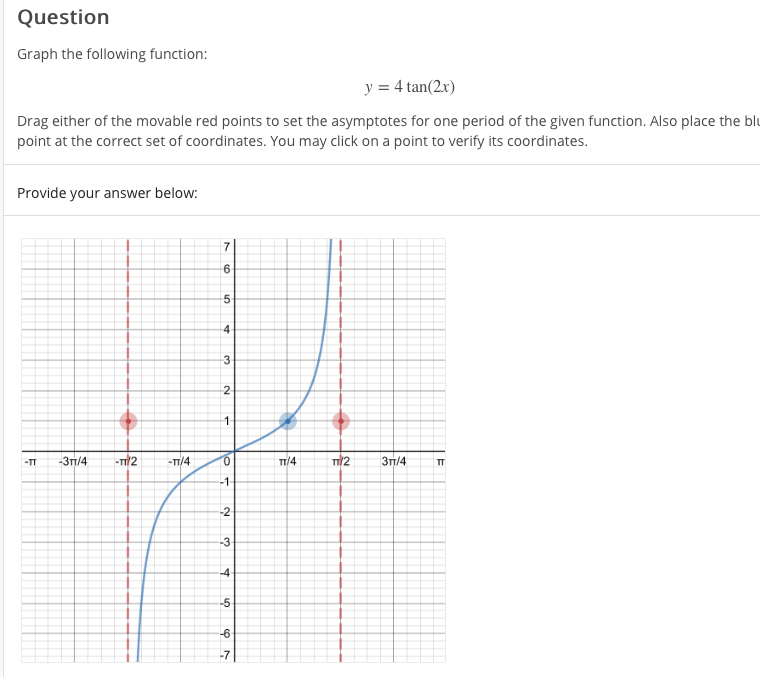
Question Graph The Following Function Y 4 Tan 2x Chegg Com

5 7 The Tangent Function Functions Siyavula

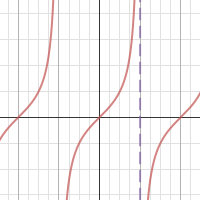
Tan Graph

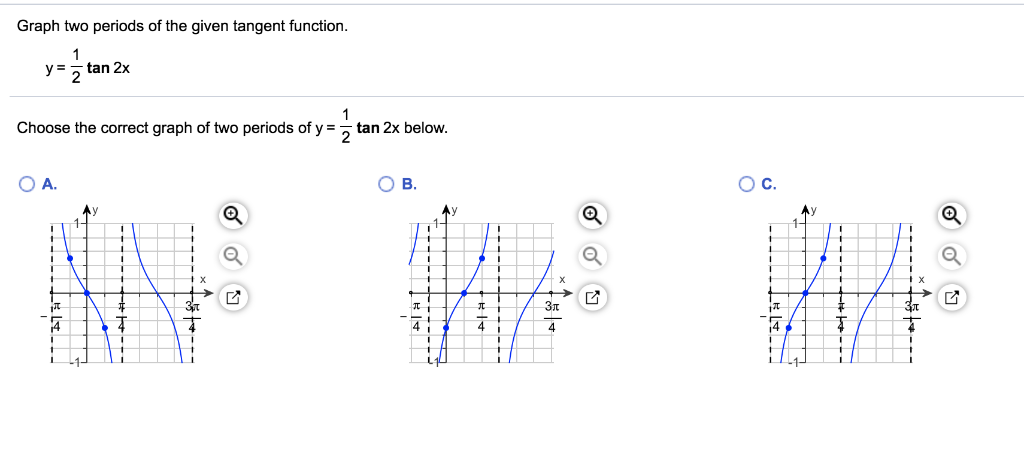
Graph Two Periods Of The Given Tangent Function Y Chegg Com

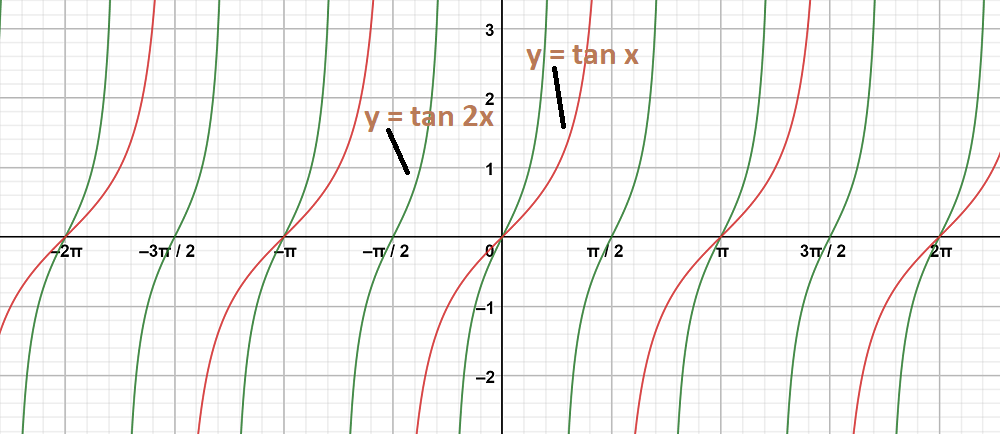
Class 11 Rd Sharma Solutions Chapter 6 Graphs Of Trigonometric Functions Exercise 6 3 Geeksforgeeks

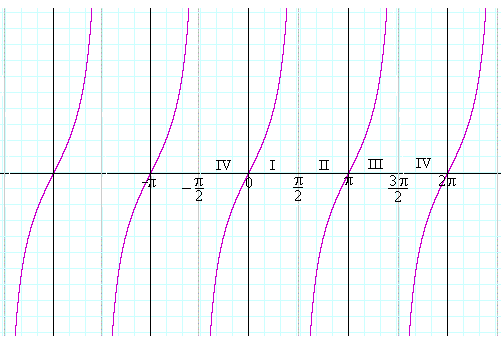
Graphs Of Trigonometric Functions

Find The Roots Of The Function Mathematics Stack Exchange

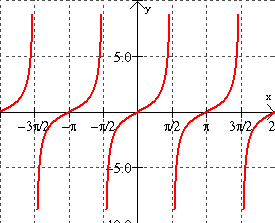
Tangent Cotangent Secant And Cosecant Graphs Mathbitsnotebook Ccss Math

Plot The Graph Of Y Tan 2x Pi 12 Maths Trigonometric Functions Meritnation Com

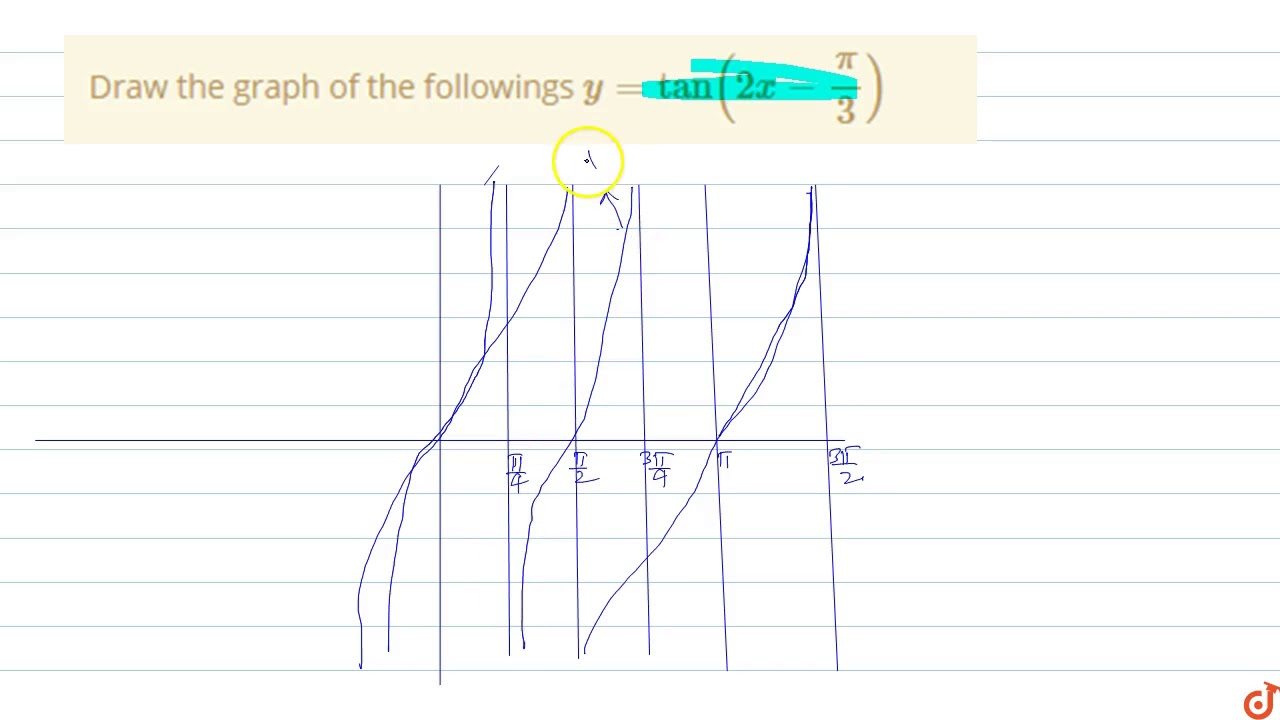
Draw The Graph Of The Followings Y Tan 2x Pi 3 Youtube

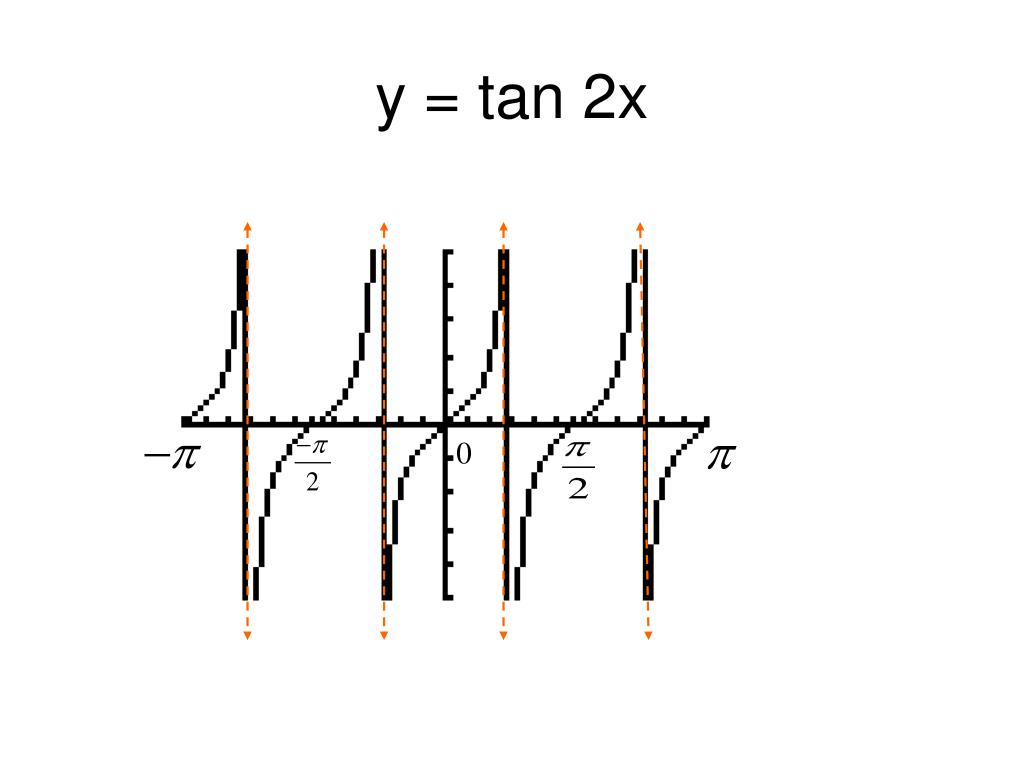
Ppt Graphing Tangent Powerpoint Presentation Free Download Id

1

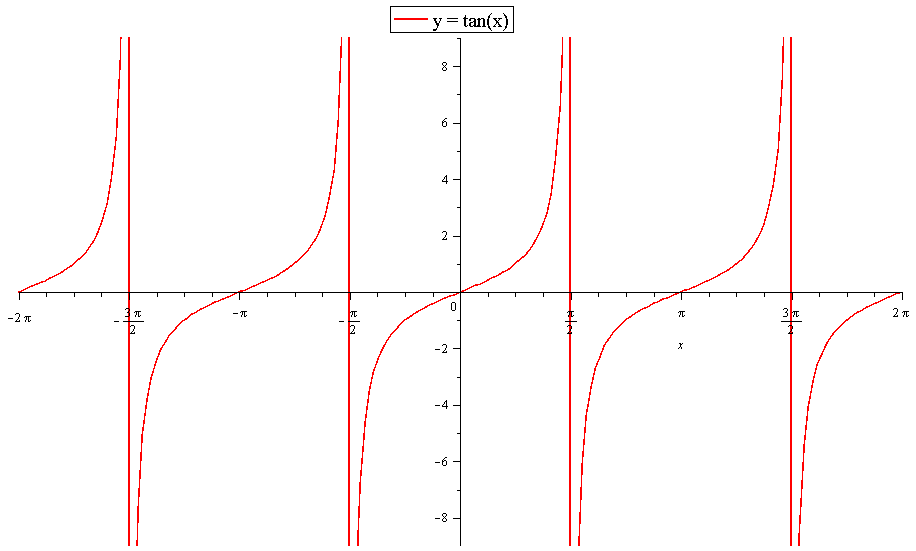
How Do You Graph Y Tan3x Socratic

Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints

Solve Tan X Tan 2x Tan 3x Tan X Tan 2x Tan 3x Blurtit

Www Edubuzz Org Prestonlodge Wp Content Blogs Dir 376 Files 16 11 Nat5maths Cmtopic21 Pdf

1

Ppt Graphs Of Other Trig Functions Powerpoint Presentation Free Download Id

Graphs Of The Other Trigonometric Functions Precalculus Ii

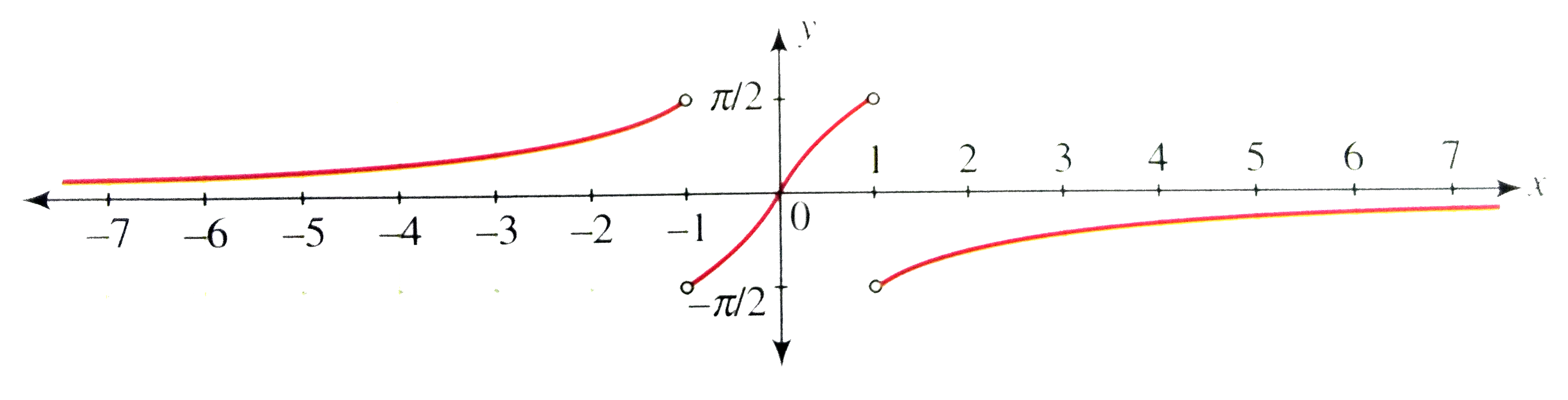
Draw The Graph Of Y Tan 1 2x 1 X 2

Trigonometric Graphs And Transformations Tan And Cot Pages 1 4 Flip Pdf Download Fliphtml5

How Do You Graph Y Tan X 3 And Include Two Full Periods Socratic

Http Lhsprecal Weebly Com Uploads 5 9 8 2 More Trigonometric Graphs Pdf

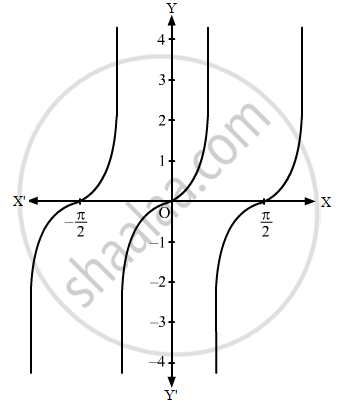
Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com

Class 11 Rd Sharma Solutions Chapter 6 Graphs Of Trigonometric Functions Exercise 6 3 Geeksforgeeks

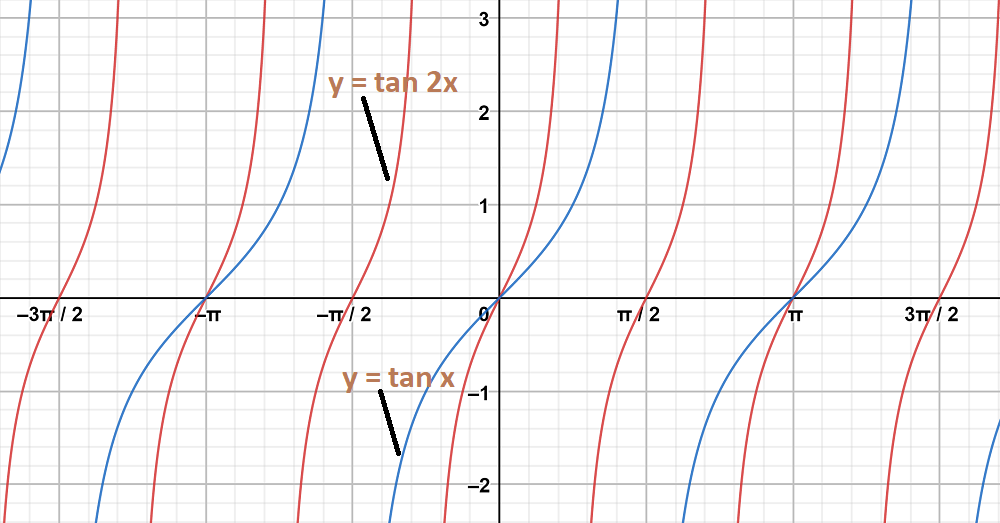
Chapter 7 Trigonometric Functions The Sine Function Imagine

On Which Interval Is The Tangent Function Invertible Mathematics Stack Exchange

Biomath Trigonometric Functions

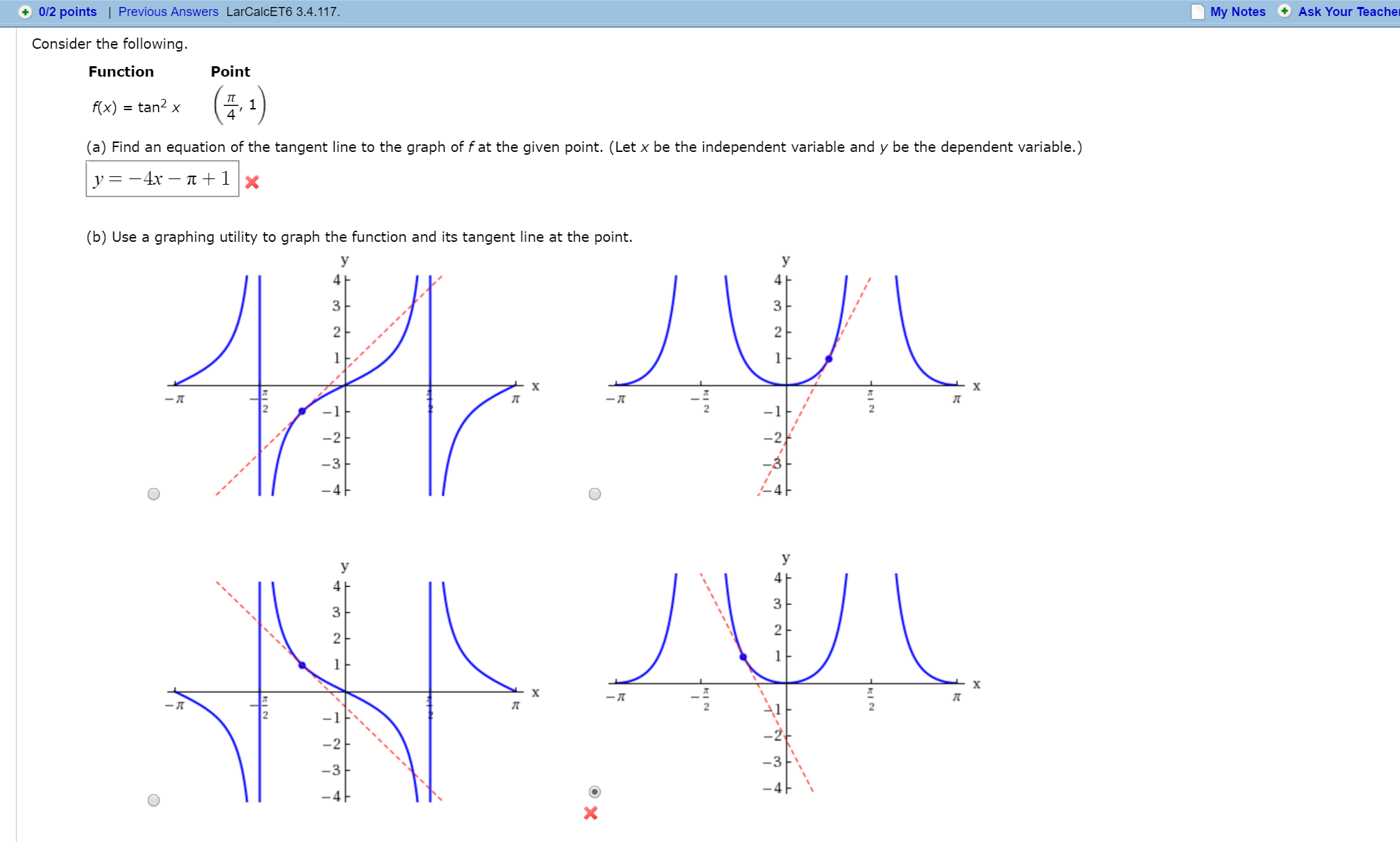
Consider The Following Function F X Tan 2 X Point Chegg Com

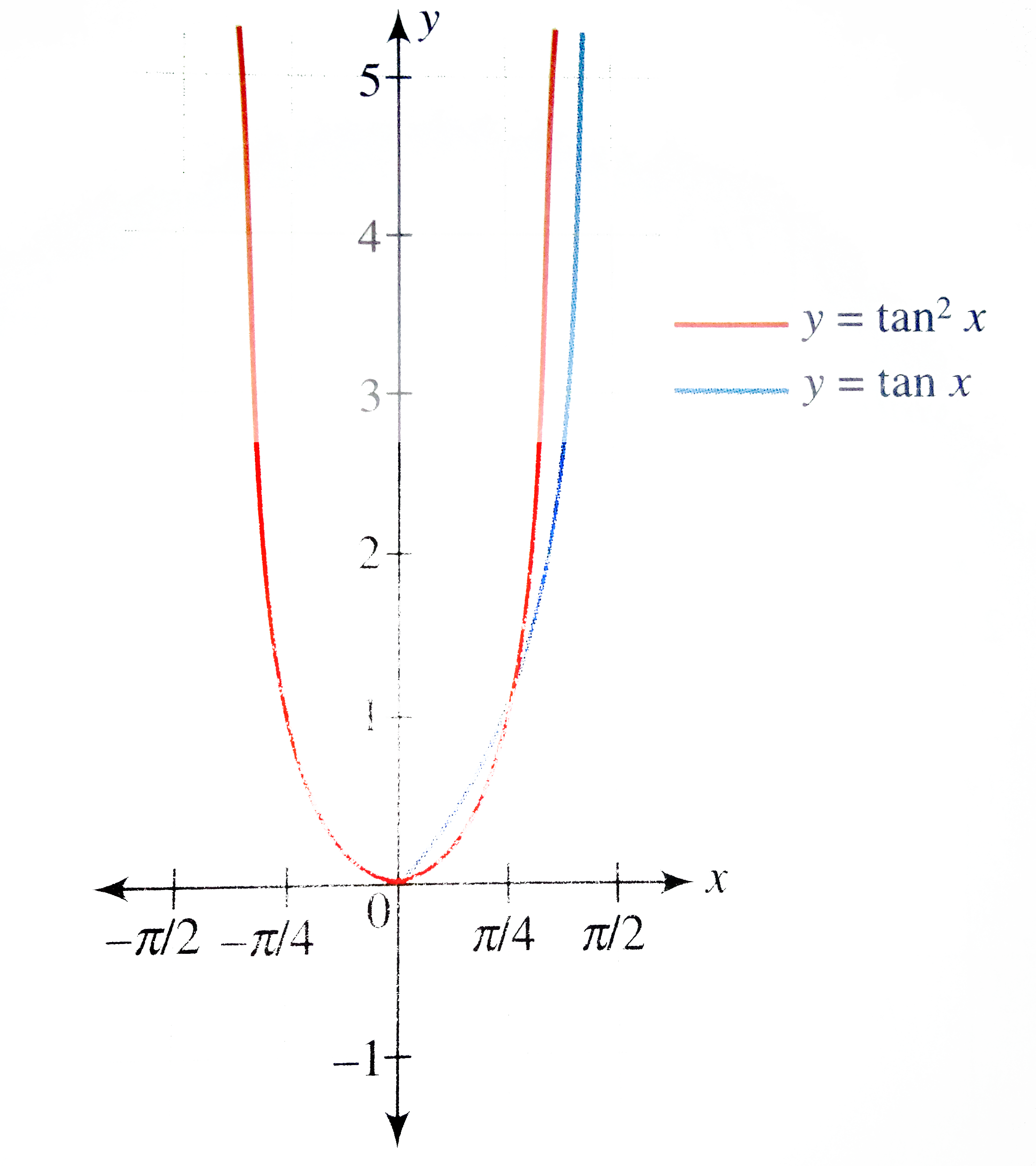
Draw The Graph Of Y Tan 2 X

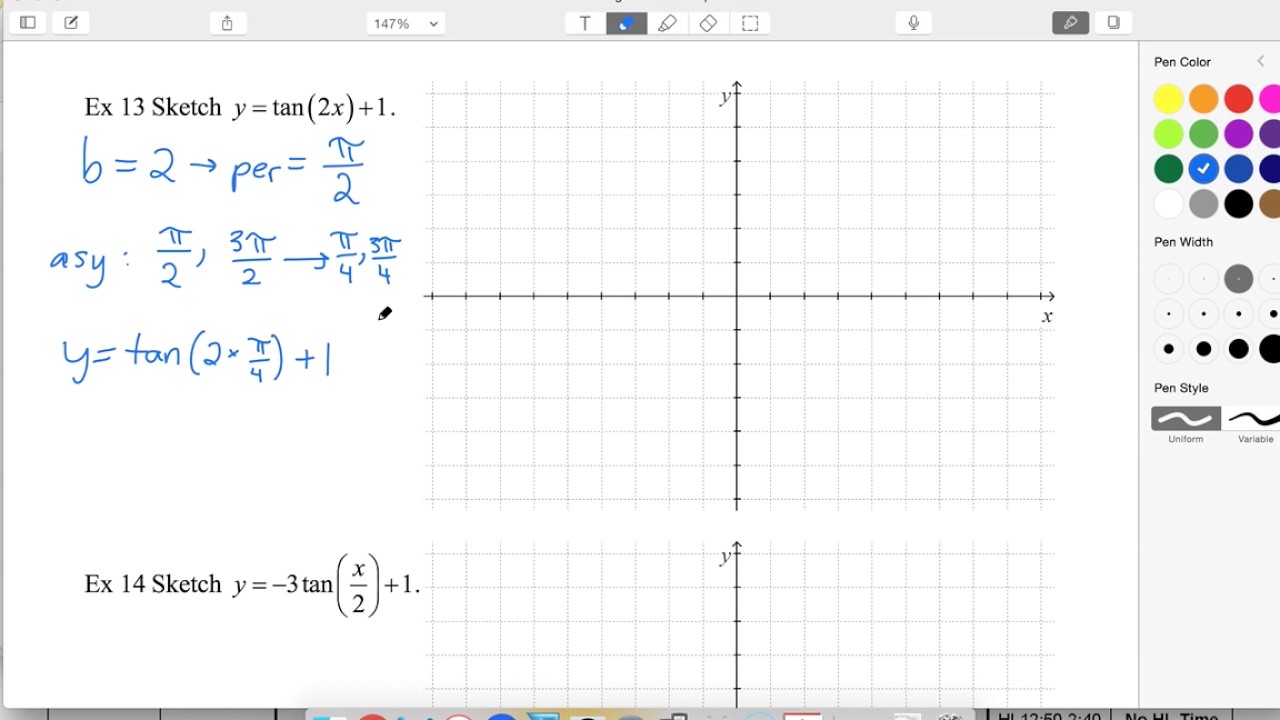
01 Ex13 Sketch Y Tan 2x 1 Youtube

Sketch The Graph Of The Following Function On The Same Scale 10 Y Tan 2x Y Maths Meritnation Com

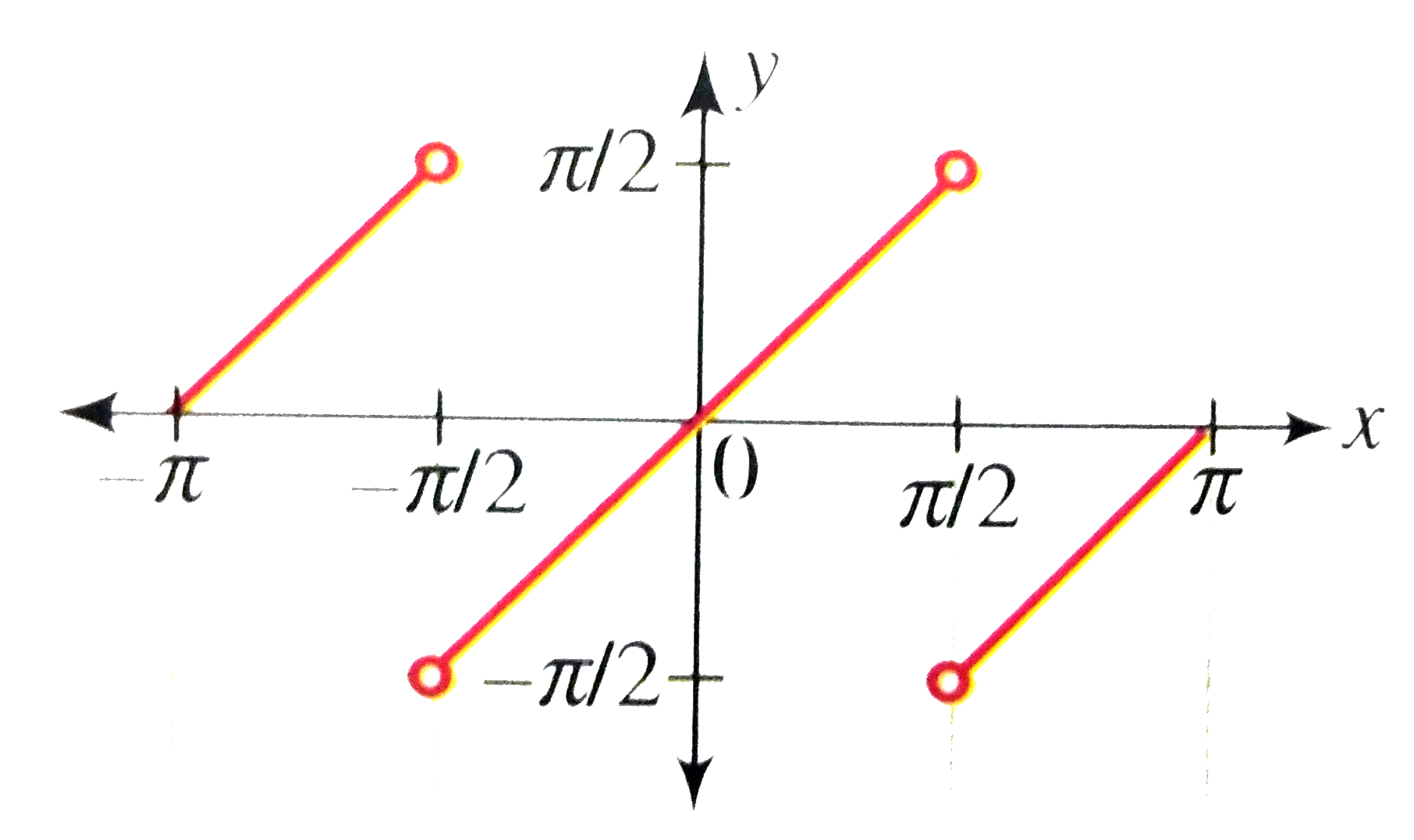
Draw The Graph Of Y Tan 1 2x 1 X 2

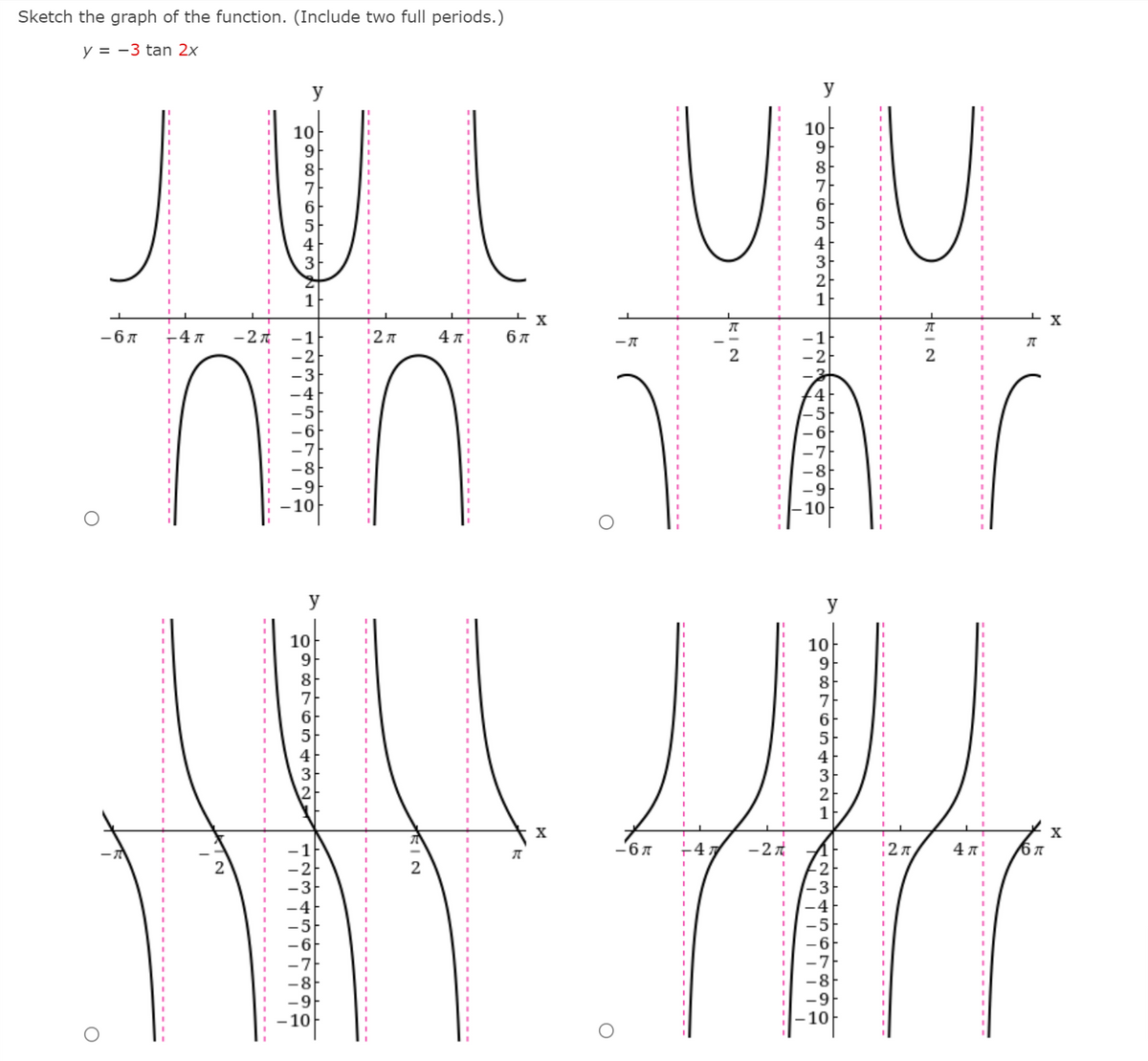
Answered Sketch The Graph Of The Function Bartleby

1

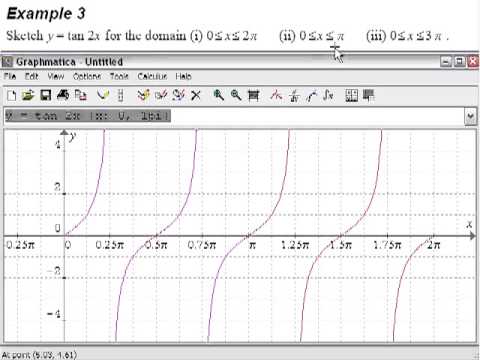
6 Trigonometry Graph Example 3 Sketch Y Tan 2x Youtube

Bestmaths

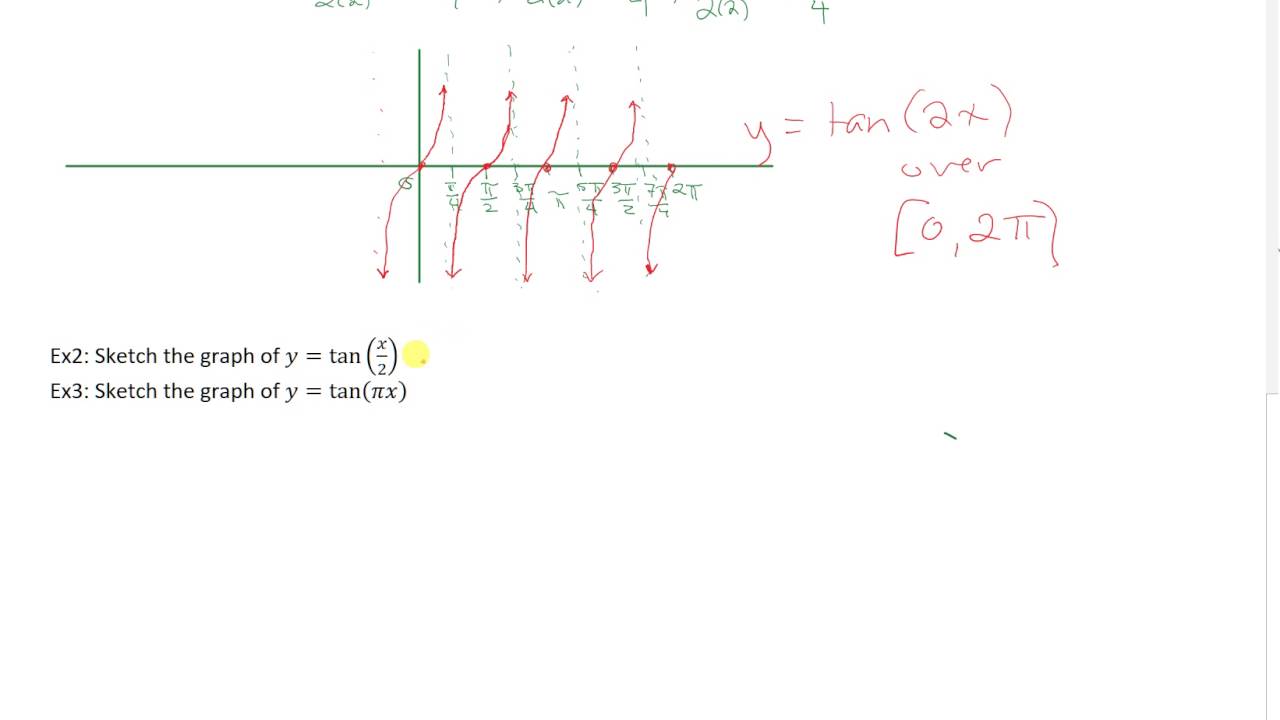
Sketching Y Tan 2x And Y Tan X 2 Youtube

What Will Be The Graph Of Y Tan X From X P 2 To X P 2 Quora

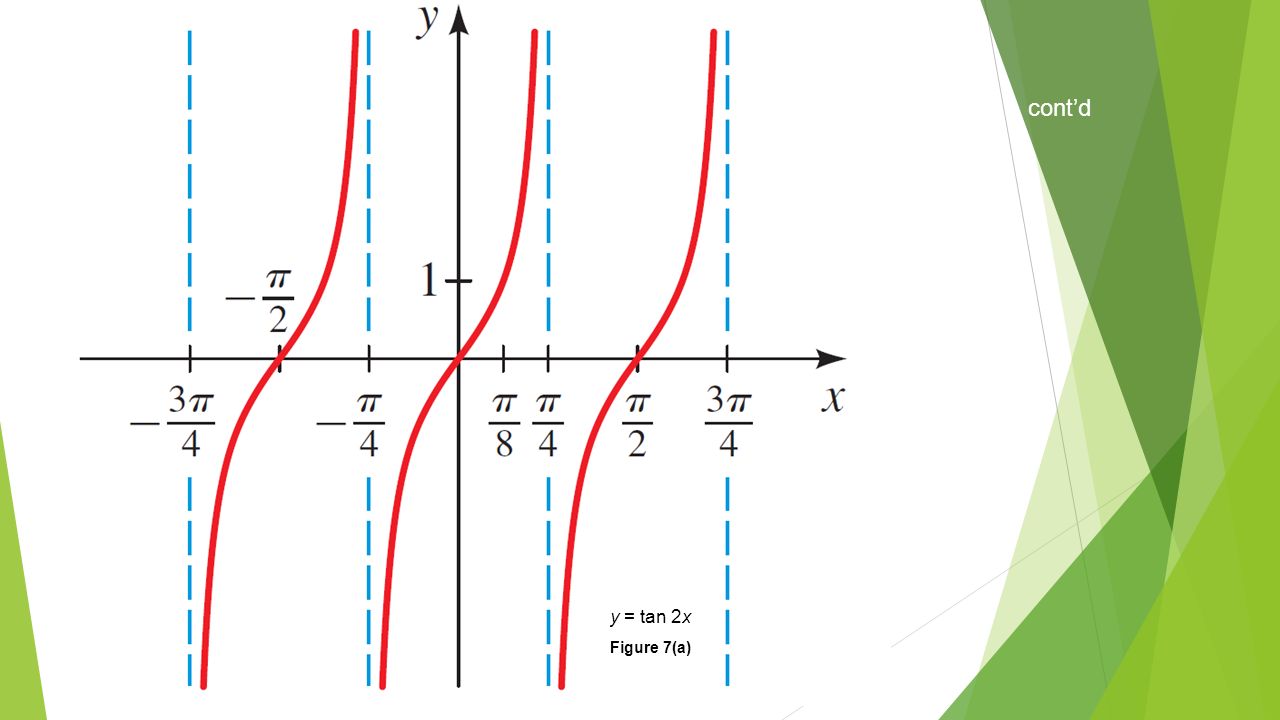
Find The Period Of Tan 2x Class 10 Maths Cbse

Graphs Of Tangent Cotangent Ppt Video Online Download

Www Interborosd Org Site Handlers Filedownload Ashx Moduleinstanceid 79 Dataid 89 Filename 4 6 graphs of other trig functions Pdf

Graphs Of The Other Trigonometric Functions Precalculus Ii

Graph Tangent And Cotangent

Tangent Graph

Tan Graphs Circular Functions

Draw The Graph Of Y Tan2x Y Tan3x And Y 2cot2x Maths Trigonometric Functions Meritnation Com

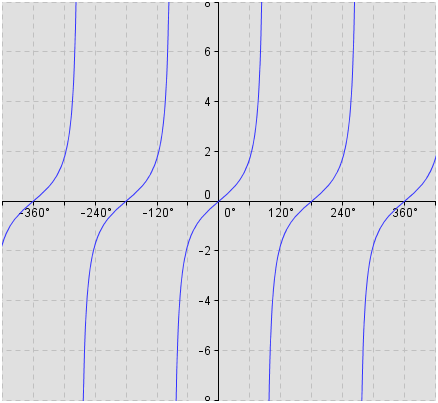
Trigonometry Trigonometric Functions

Long Question 3 User S Blog

4 Graphs Of Tan Cot Sec And Csc

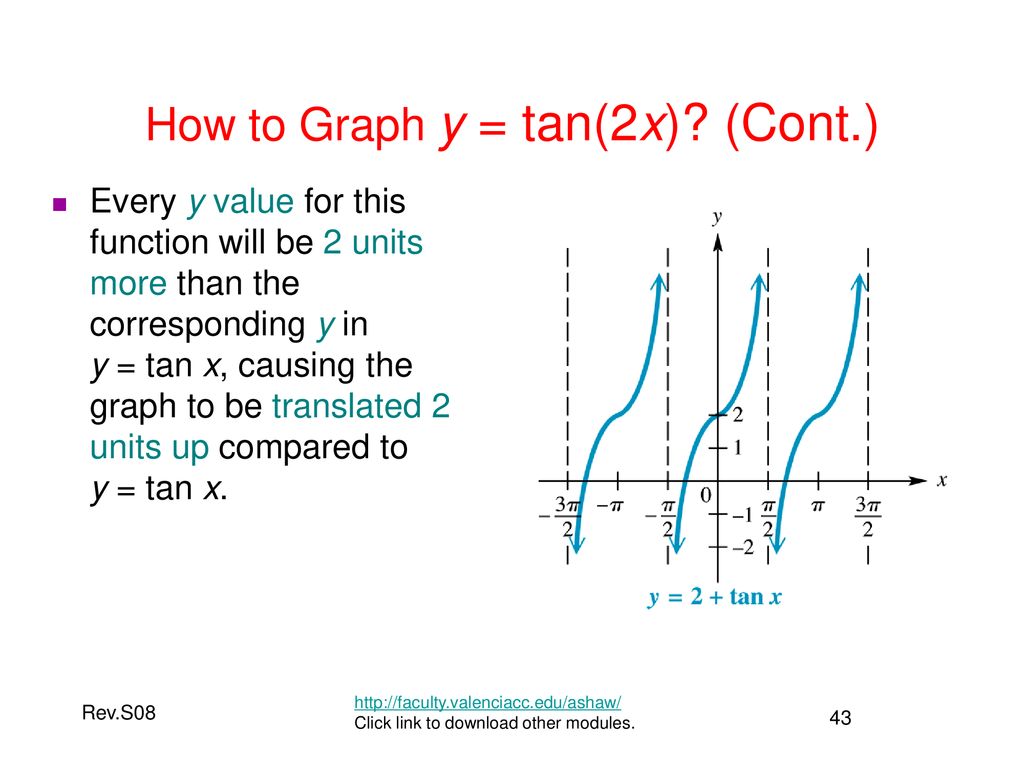
Graphs Of The Circular Functions Ppt Download

What Is The Graph Of Mod Of Tan X Quora

Graphs Of The Other Trigonometric Functions Precalculus Ii

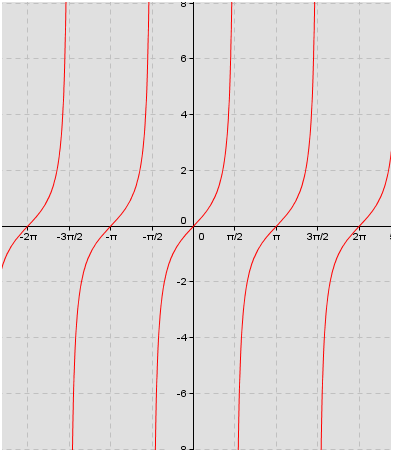
Trigonometry Trigonometric Functions

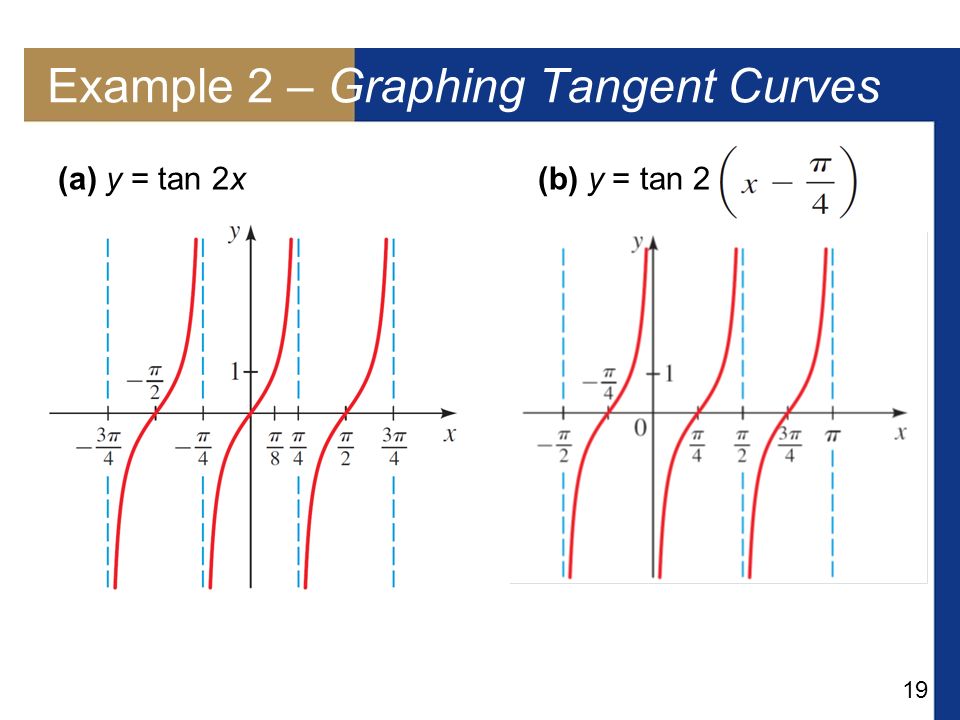
More Trigonometric Graphs Ppt Download

How To Graph Tan Ex Y Tan2x Study Com

Graphing Transformations Of Tangent Functions Flashcards Quizlet

Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Download

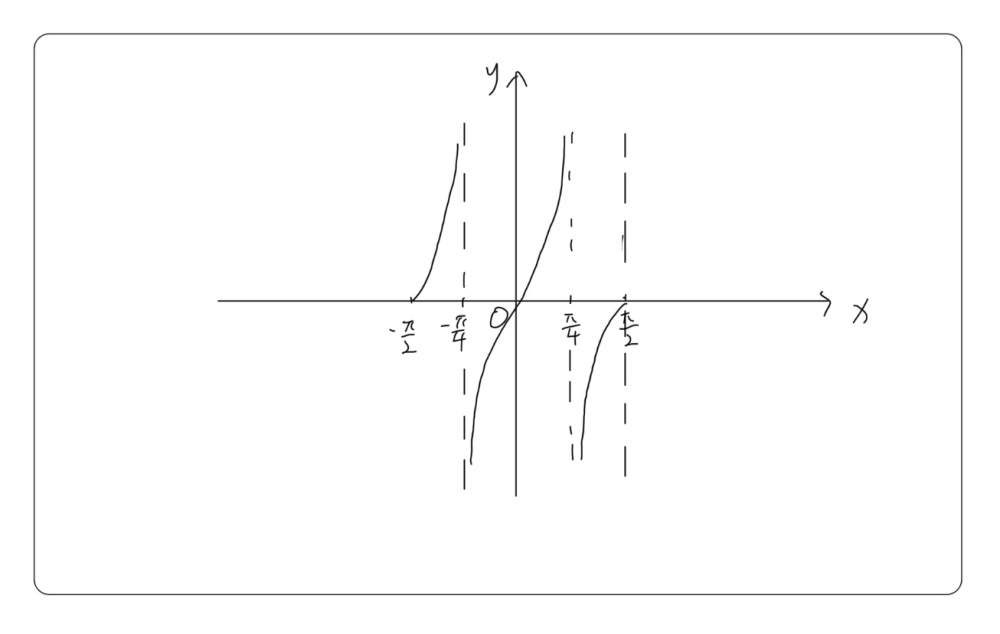
10 Graph Y Tan 2x Over The Intervall 90 Gauthmath

Solution Determine The Period Of Y Tan 2x

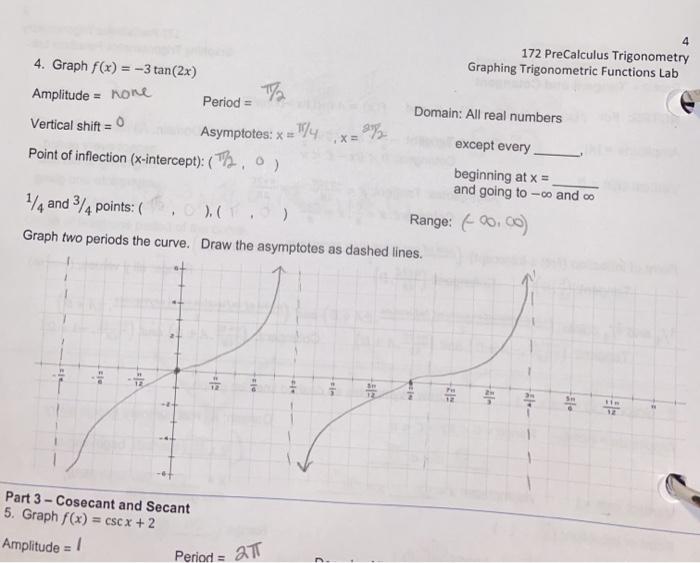
More 72 172 Precalculus Trigonometry Graphing Chegg Com

Sketch The Graph 1 Y Cos 2 X 2 Y Tan2x 3 Y Sin2x Maths Trigonometric Functions Meritnation Com

Graphing Tangent Functions

5 7 The Tangent Function Functions Siyavula

Please Graph The Following Functions In A Separate Piece Of Paper I Y 3 Tan Homeworklib

Graphs Of The Tangent And Cotangent Functions

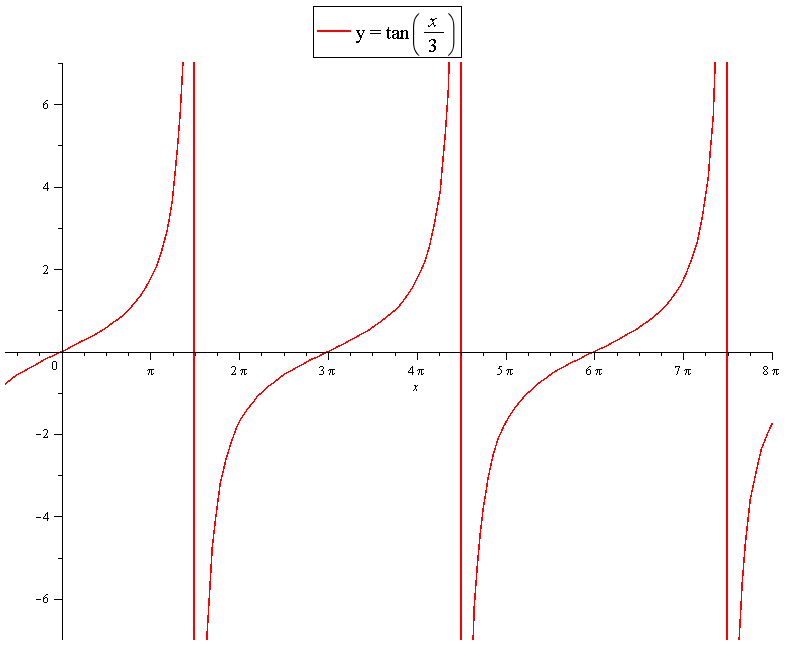
How Do You Graph Y Tan X 3 And Include Two Full Periods Socratic

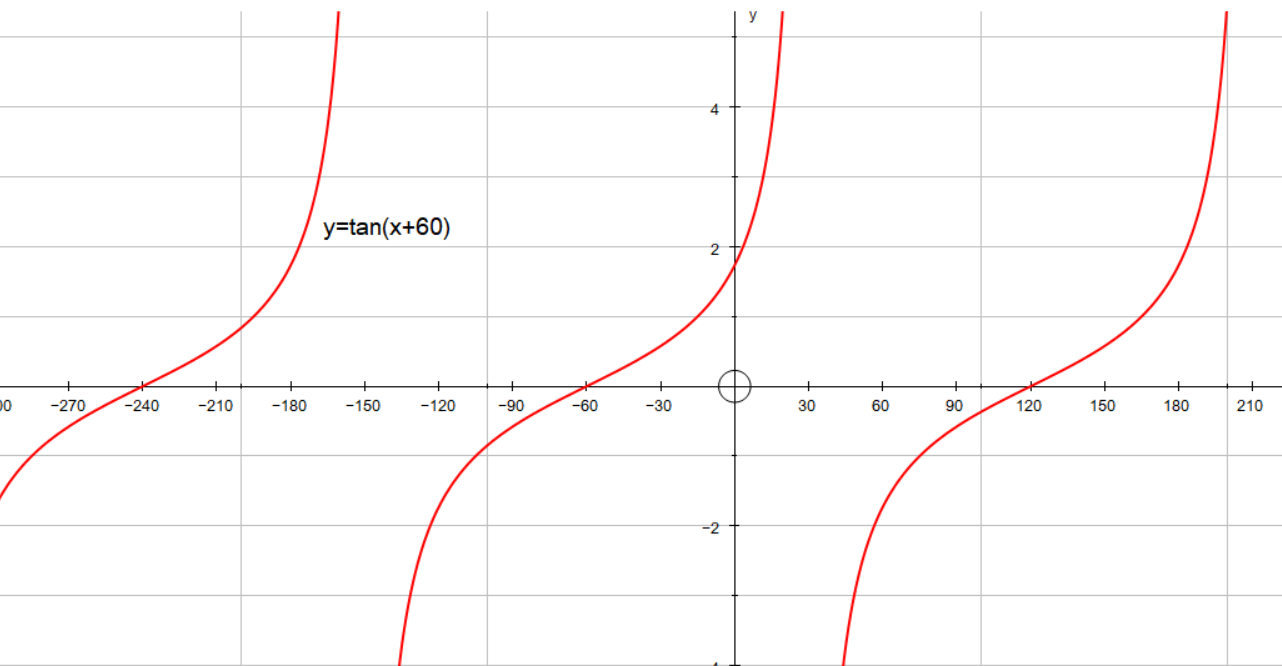
How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic

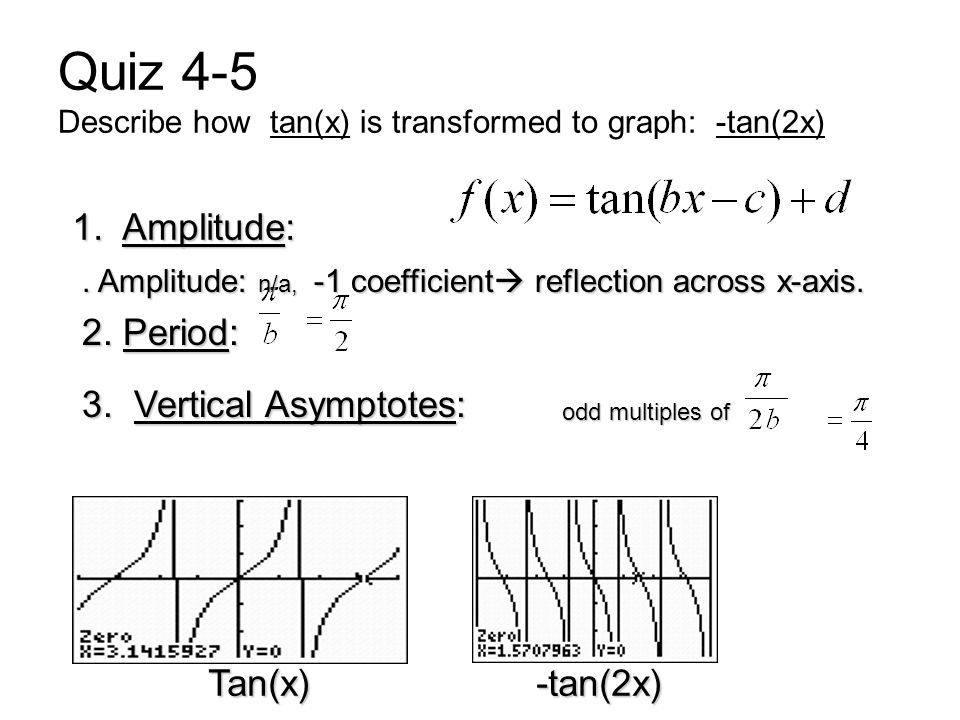
Quiz 4 5 Describe How Tan X Is Transformed To Graph Tan 2x Ppt Download

Incoming Term: tan 2x graph, tan 2x graph radians, tan 1/2x graph, y=tan(2x) graph, y 3 tan 2x graph,